Determining the surface area of part of a sphere🔗

Determining the surface area of a sphere turns out to be way way easier than it seems like it should be. You do a big integral, but then everything cancels out and it’s ... pretty amazing. Let me see if I can explain this.

1 Simplifying the problem🔗

The first thing to do is to simplify the problem. Specifically, let’s get rid of the "east/west" part of the problem. If we ask for the surface area of a region of the earth from 10° North up to 20° North, and from 30° West up to 60° East, then the "east-west" extent of this rectangle is 90°, which is just a quarter of the way all the way around the sphere. In other words, if we can determine the surface area of the region from 10° North up to 20° North all the way around the sphere, we just need to divide by 4 (or, equivalently, multiply by 90/360), and we’re done.

So now all we need to do is figure out the surface area of a region of the sphere, "sliced horizontally".

2 The Calculus Part🔗

Okay, so this is a definite integral. It turns out that for our purposes, we are best off taking this integral with respect to , the distance above the equator (measured along the axis).

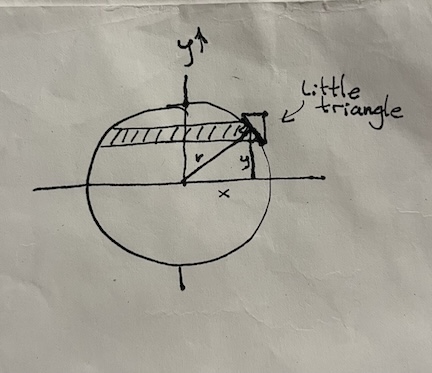
Let’s say the shaded band is from up to .

The surface area of a cylinder with radius and height is known to be , so if we just naively model this as a stacked set of cylinders, we get the integral

... where is the radius of the sphere at a particular height .

But wait! We’re modeling the surface of a curved, convex shape, here, and that means that when we do this integral, we need to include a multiplier to compensate for the fact that an angled surface is longer (per unit ) than a vertical surface. This becomes quite extreme at the top of the sphere, where the surface is nearly horizontal. If we were to model this using a sequence of purely-vertical "shells", we’d be missing a big chunk of the area.

What is this multiplier? Well, it’s the ratio of the length of the slice to the vertical extent of that slice. Take a look at that "little triangle" in the diagram. The ratio of the hypotenuse of that triangle to the vertical side of that triangle is the multiplier in our integral.

Hmm... but ... because the hypotenuse of that small triangle is perpendicular to the line labeled , that small triangle is similar (in the geometric sense: same side ratios) to the main inner triangle, the one with sides , , and . So the the ratio of the hypotenuse to the vertical side of the small triangle is the same as . This means that our integral should be

Well, this suddenly got a whole lot simpler. The cancels out! So the integral is just

... and since all of these are constants, the definite integral is just

Wow! That’s some really amazing cancellation.

To double-check, we can take the extreme condition when is at the top of the sphere and is at the bottom. In other words, when . In this case, the surface area turns out to be , which is what the textbooks tell us is true.

3 Taking this back to Earth🔗

Okay, so now all we have to do is get the units right. Make sure that your radius and y values are both in km, figure out how to convert latitude angles into km above (or below) the equator, and use the east and west longitudes to take a fraction of that full ring.

As a sanity check, it might be useful to know that at the equator, a "minute" (that is, 1/60 of a degree) is about one nautical mile, so a square area of width one degree and height one degree near the equator would be about 3600 square miles.